柳学智

[摘要]  由于考试分数对于应试人员的重要性，同时也由于原始分数难以服从正态分布，考试分数不适合进行正态转换，为了保持转换过程中的信息守恒，应采用线性转换的方法进行分数转换；由于各科平均差决定各科分数合成的权重，应先通过分数转换将各科分数的平均差取齐，然后再选择学科外部或内部方法确定各科权重，在此基础上将各科分数合成为总分。

[关键词]  大规模考试  分数转换  分数合成

一、问题的提出

当今社会，在评价、筛选、提拔、录用等情景下，人们开发使用了各种不同的考试，并依据考试分数进行决策。在大规模考试中，由于考试规模巨大，应试人员众多，任何微小的分数差异，都可能影响对一部分应试人员的决策。

在多科考试中，每个科目都有一个考试分数，经常需要将各科分数进行转换，然后合成总分。在此过程中，依据不同的方法进行分数转换与合成，考试分数会发生较大变化，进而影响对应试人员的决策。因此，分数转换与合成的合理性直接影响决策的公平性。

那么，考试分数转换与合成过程中都有哪些常用的方法？它们的使用有哪些条件？如何评判各种方法的合理性？本文从考试所测量的构念出发，通过分析考试分数转换与合成过程中的常见误区，找出合适的解决方法。

二、分数转换中的误区分析

分数转换的目的是为了比较应试人员个体或群体在不同科目上的水平差异，但利用原始分数进行比较时，存在着严重的缺陷，主要表现在两个方面：一是总体平均水平不等，使得评价没有统一的出发点；二是总体离散程度不一致，使得评价没有统一的尺度。

为比较应试人员在不同科目上的水平差异，必须假定各科所测构念在总体分布上，平均水平相等，离散程度一致。原始分数总体所表现出来的平均水平不等和离散程度不一致，是由于考试题目样本的代表性、原始分数全距的局限性等造成的，可以通过分数转换，将原始分数转换成导出分数，使得导出分数的平均水平相等，离散程度一致。这样，依据导出分数，可以对应试人员在不同科目上的水平差异进行比较。

在考试分数转换中，有两种转换方法：一种是按正态分布的分布概率将原始分数转换成对应的导出分数，简称为正态转换；另一种是将原始分数按照一定参数进行线性变换，转换成适合形式的导出分数，简称为线性转换。

要使分数转换达到上述目的，需要排除转换过程中无关因素对所测构念的影响，下面通过对分数转换方法的适用条件、假设前提、转换过程等的分析，澄清分数转换中的各种模糊认识，进而找出合适的分数转换方法。

㈠正态转换的适用条件

在统计分析中，经常进行样本推断，有时数据拟合性较差，为了研究方便，将描述该对象的测验分数或观察数据进行正态转换，转换成合适的数据形式，再进行数据拟合，找出统计规律，据此推断总体趋势。在样本推断中，之所以进行正态转换，是由于研究条件的限制，所采集的样本量小，代表性差，样本数据不服从正态分布，在假设研究对象服从正态分布的前提下，进行正态转换，使转换后的数据服从正态分布，然后依据此数据寻找统计规律。在此过程中，关注的重点是寻找统计趋势，进行分数转换后，转换前后分数的差异对应试人员个体不会产生任何影响，进行正态转换是合适的。

但是在考试的情景下，考试分数是对应试人员的测量结果，是对应试人员个体水平的统计描述，考试分数对应试人员具有极端重要性。分数转换的目的是为了比较应试人员的水平差异，在分数转换中，如果原始分数不服从正态分布，进行正态转换后，转换前后的分数会产生转换差异，原始分数分布与正态分布之间差异越大，转换差异越大。由于考试分数的微小差异都可能影响对一部分应试人员的决策，转换差异可能对应试人员个体产生严重影响，进而影响决策的公平性，因此，考试分数难以适用正态转换。

㈡原始分数的分布

在进行正态转换时，实际上假定一个前提，即原始分数服从正态分布。考试分数服从正态分布应满足两个条件：一是考试所要测量的构念的分布是正态的，二是考试设计对分数分布的要求是正态的。从统计上，在大规模考试中，由于应试人员人数众多，可以假定构念的分布是正态的，但是从每一考试设计来看，是否都要求每一科目的考试分数服从正态呢？无论是常模还是准则参照性考试，如果某一科目考试需要划定合格分数线，合格线以上或以下的应试人员无须仔细区分，为了提高区分精度，减少决策误差，应重点区分合格线附近的应试人员，使得合格线附近的人员尽可能少，分数分布应出现一个分布低谷，如果有多条合格线，理想状态下应对应出现多个分布低谷。因此，分数分布应与一定的合格分数线相联系，在不同的考试中，录取率不同，合格分数线也不相同，对分数分布的要求也不一样，因此，从考试设计上不能要求每一科目考试分数服从正态分布。

从试卷难度看，分数分布还与试卷难度有一定关系，试卷难度又与应试人员的总体水平相联系。由于受试卷满分的限制，每一科目的分数全距总是有限的，分数分布不能向两端无限延伸，同时由于受到给分点数量的限制，在有限的分数全距内不能无限细分。当试卷难度偏难时，大部分应试人员得分较低，分数分布不能向下无限延伸，集中在低分端，容易形成正偏态；与之相反，当试卷难度偏易时，大部分应试人员得分较高，分数分布不能向上无限延伸，集中在高分端，容易形成负偏态。在很多考试中，试卷难度都是凭经验控制的，很难保证试卷难度与应试人员的总体水平完全吻合，因此，从试卷难度控制上也不能要求每一科目考试分数服从正态分布。

从原始分数的实际分布看，我们选择了1999年11个资格考试的32个科目的全国数据，计算出每个科目的偏态系数，从整体来看，大部分科目的偏态系数为负，小部分为正，其中偏态系数小于-0.3或大于0.3的科目约占全部科目的70%，从统计上，这些科目的分数分布就不是正态分布。

㈢非正态分布下的正态转换

当原始分数不服从正态分布时，强行进行正态转换会产生哪些后果？下面从信息传递的角度，分析在原始分数的非正态分布下的正态转换过程。

不同的测量结果具有不同的精确性，根据测量结果的精确性，测量数据分为四类：称名数据，定性地区分出不同的事物；顺序数据，在称名数据所含信息量的基础上，排列出事物的顺序；等距数据，在顺序数据所含信息量的基础上，度量出事物之间的差距；比例数据，在等距数据所含信息量的基础上，度量出事物的绝对量。测量数据所含信息量按称名、顺序、等距、比例数据的顺序递增。

从测量数据的精确性上，原始分数含有多少信息量？属于哪一类测量数据？在我国当前大多数大规模考试中，测量结果是依据经典测量理论用原始分数表示出来的，在计算每一科目的原始分数时，将每题得分直接相加，得出科目总分。虽然分值相同的题目可能有不同的难度，相同的分数可能有不同的“含金量”，但在计算科目总分时，并没有考虑这些因素，依然认为它们是相同的，直接相加。从数据可加性上，称名、顺序数据不能直接相加，等距、比例数据可以直接相加，可以认为原始分数可能是等距或比例数据。同时，原始分数测量的是应试人员之间的差异量，并非应试人员的绝对量，某一应试人员在某一科目考试上得零分，并不能认为他在该科目上的水平或能力是零，只是因为这次考试不能测量出其水平或能力，因此，原始分数的零点是相对的，不是绝对的。综上所述，可以认为原始分数是一种等距数据。

分数转换是从一种分数转换成另一种分数，从信息传递上，从A分数转换为B种分数，A分数中的信息要完整准确地传递到B分数，在信息传递过程中，这两个分数之间的信息应保持守恒，既不能增加，也不能减少，更不能改变。由于不同的测量数据所含信息量不同，要保持分数转换过程中的信息守恒，转换前后的分数应是同一类型数据，即要么是称名数据，要么顺序数据，要么等距数据，要么比例数据。只有保持了分数转换中的信息守恒，分数转换才能可逆，既可以正向转换，又可以逆向转换。原始分数作为一种等距数据，要保持分数转换中的信息守恒，转换后的分数也必须是等距数据。

考试分数的正态转换过程为：将某一科目所有应试人员的考试分数从大到小排序，计算每一个分数以下的应试人员人数占应试人员总数的百分比P，利用百分比P查正态分布表得正态Z分数，进行线性变换，以适合形式的平均分和标准差计算得到所需形式的标准C分数。

正态转换过程实际上包含三次转换，第一次转换是将每一学科的原始分数从高分到低分排列成百分等级，转换的结果是百分等级。原始分数是等距数据，百分等级是顺序数据，这样丢失了原始分数之间的差距信息，而只保留分数之间的顺序信息。通过考试测得的描述应试人员的信息量减少了，第一次转换没有保持信息的守恒。

第二次转换是在得到百分等级后，由百分等级查正态分布表，得到正态化Z分数，转换的结果为Z分数。百分等级是顺序数据，Z分数是等距数据，这样重获差距信息，但该差距信息并不是考试所测得的，不反映应试人员之间的真实差距，而是以百分等级为基础，以完全理想的正态分布为依据重新赋予应试人员的，由于原始分数并不服从正态分布，这些信息是变化了的信息，第二次转换也没有保持信息的守恒。

第三次转换是进行线性变换，根据Z分数，以一定平均分和标准差计算得到所需形式的标准C分数，转换的结果为C分数。Z分数是等距数据，C分数也是等距数据，第三次转换保持了信息的守恒。

综上所述，从信息传递上，原始分数是等距数据，同时包含顺序信息和差距信息，分数经过第一次转换，保留了顺序信息，丢失了差距信息，信息减少了；经过第二次转换，仍保留了顺序信息，获得了差距信息，但该差距信息是根据正态分布重新赋予的，差距信息变化了；经过第三次转换，信息得以完整准确地传递，而此时分数所真正包含的信息只剩下顺序信息了。

㈣线性转换分析

从上述分析看，当原始分数难以服从正态分布时，正态转换会产生较大误差，会对应试人员的决策产生严重影响，那么在非正态分布下该如何转换考试分数？我们认为应选择线性转换。

线性转换不受原始分数分布的限制，无须正态分布假设，在任何分布形态下都可以进行线性转换，适用范围十分广泛。在线性转换中，仅对原始分数作线性变换，假定原始分数为X，导出分数为Y，线性转换可以写为Y＝AX＋B，其中A（A＞0）为斜率，改变原始分数的离散程度，B为截距，改变原始分数的平均水平，这样通过改变原始分数的平均水平和离散程度，可以使导出分数的平均水平相等，离散程度一致，能够达到分数转换的目的。从转换过程看，原始分数是等距数据，经过线性转换后，得到的导出分数也是等距数据，转换过程中保持了信息的守恒。

在考试实践中，为了将原始分数转换成需要的形式，往往要进行两次转换。第一次将原始分数转换成Z分数，即将原始分数减去其平均分后，再除以标准差，这一过程也是线性转换，导出分数为Z分数，平均水平为0，离散程度由标准差表示，数值为1。第二次以Z分数为基础，以A（A＞0）为单位，以B为平均数，再将Z分数转换成C分数，即C＝AZ＋B，在具体考试中，根据实际需要，将A、B取一定的值，把分数转换成需要的形式。比如T分数的平均分为50，标准差为10，CEEB（College Entrance Examination  Board，美国大学入学考试委员会）分数的平均分为500，标准差为100。

三、分数合成中的误区分析

在进行多科考试分数合成前，首先面临考试分数的可加性问题。有人认为，不同科目的考试测量的是不同的构念，不同的构念在本质上是不同的，反映不同构念的考试分数虽然在表面上是一样的，但不能相加合成，强行将不同科目的考试分数相加合成，得到的合成分数含义不明确，性质不确定。也有人认为，在同一考试的不同考试科目中，尽管不同科目的考试测量的是不同的构念，但这些构念之间是相关的，有时甚至相关程度很高，每一科目所测量的构念只是一个更大构念的一个侧面，不同科目的考试就像同一个测验中的不同分测验，其分数是可以相加合成为总分，只有总分才反映考试所测量构念的全貌。在考试实践中，有时必须将多科考试分数合成为一个总分，才能依据该总分作出相应的决策。

原始分数转换成导出分数后，为各科分数的比较提供了统一的基准，但也使分数合成中的权重问题显现出来：在原始分数合成中，直接将各科分数相加合成，忽视了各科权重的存在，或者直观地认为各科的权重可以通过科目满分来实现；在导出分数合成中，由于取齐了各科导出分数的离散程度，各科在分数合成前具有相同的地位，各科分数以相同的权重直接相加合成？还是以不同的权重进行合成？权重问题显现出来。

在分数合成中，究竟有哪些因素影响各科权重？如何确定各科目的权重？在这些问题上往往存在认识误区，直接影响分数合成的合理性。

㈠影响科目权重的因素

在合理确定各科权重前，应探明在分数合成中影响各科权重的因素。显而易见，各科的平均分是一个因素。某一科目的平均分越高，在总分中所占的比例越大，所起的作用也越大。但平均分的作用是面向全体应试人员的，平均分高，全体应试人员的分数都高，应试人员之间的差距并没有改变。在合成总分中，某一科的平均分高低，相当于在总分中给所有应试人员为该科目加上或减去一个常数，并不能改变应试人员在总分上的差距。在准则参照性考试中，这一常数可能会改变合格分数线的划定，平均分的作用会表现出来；但在常模参照性考试中，在总分中为某一科目加上或减去一个常数，不能改变应试人员在总分中的排序，也不能改变合格率，各科目平均分并不起作用。

除了平均分以外，还有哪些因素影响各科权重？在分数合成中，为了探讨其它因素对各科权重的影响，需要先消除平均分的影响。如何消除平均分对分数合成的影响呢？可以将各科的平均分置为0，即将每一原始分数减去其平均分，得到离差。排除平均分的影响后，合成各科分数相当于合成各科离差，由于离差中有负数，需要将离差取绝对值后，变成绝对离差，再进行合成。因此，分数合成实际上是合成各科的绝对离差，绝对离差和为合成总分，各科绝对离差在绝对离差和中的比例决定了各科在合成总分中的权重，而各科绝对离差的平均值即为平均差，实际上，各科平均差决定各科在分数合成中的权重。

在分数合成中，人们常常误以为各科权重是由标准差决定的。虽然标准差与平均差都是描述离散程度的统计量，但含义不同。为了对比，我们以1999年某执业资格考试为例进行说明，该考试有4个科目，每个科目的满分为100分，各科目的标准差、平均差及其各自权重列于表1，可以看出，虽然标准差和平均差的权重十分近似，但还存在一定差异。

表1  标准差与平均差的权重对比

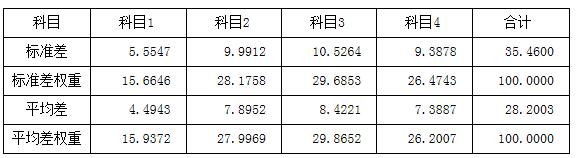
注：如果权重之和为100，各科的权重可以这样求得：以各科的值除以各科之和，然后再乘以100。例如，科目1的平均差权重为：(4.4943/28.2003)*100=15.9372。

㈡科目权重的确定方法

原始分数转换成导出分数后，由于取齐了各科导出分数的平均差，在导出分数合成中，各科权重的确定主要有两类方法：学科外部和内部方法。

1、学科外部方法

学科外部方法认为，在合成各科分数时，不同科目所测量的构念仅是整个考试所测量的构念的一个侧面，每一侧面在构念中的重要性应取决于对该构念的理解与设计，有的学科比较重要，在构念中所起作用较大，应赋予较大的权重，而有些学科的重要程度较低，应赋予较小的权重。

在确定各科权重时，有不同的方法：一是依据各科的教学或培训时数确定权重，教学或培训时数多的学科应该赋予较大的权重，在计算时，先查出每一科目的教学或培训时数，根据各科时数之间的比例确定各科目权重的比例，然后根据该比例计算出每一科目的权重；二是选择学科专家进行人工评定，根据专家知识来确定各科权重，在选择专家时应注意专家的代表性，在评定时，先让每位专家为每一科目评定一个权重，然后再计算每一科目上所有专家的平均权重，依此作为该科目的最终权重。

2、学科内部方法

当学科外部方法不适用或无法使用时，为保持考试所测构念在不同年度上的稳定，可采用学科内部方法对各科原始分数权重进行调整，使不同年度的各科权重能够统一。

在考试实践中，多年考试结果统计分析发现，不同科目的平均差的相对大小有一定的规律性，比如在高考中，数学、物理、化学、外语的平均差较大，语文、政治、历史的平均差较小。这种规律性与一定的学科特点相联系，是多种因素综合作用的结果。从所测构念上，有些学科对所测量的构念界定明确，结构层次清晰，易于测量；与之相反，有些学科对所测量的构念争议较大，难以取得共识，结构层次模糊，难以测量。从误差控制上，平均差较大的学科往往使用较多的客观性试题，试题的客观化程度较高，评分误差相对较小；与之相反，平均差较小的学科使用较多的主观性试题，试题的主观化程度较高，评分误差相对较大。从区分能力上，在分数全距和给分点相同的情况下，平均差大的学科对应试人员的区分能力强，平均差小的学科对应试人员的区分能力弱。在一定的命题情况下，这反映了学科本身所具有的特点。

在分数合成时，可根据不同学科的这一特点，给平均差大的学科以较大的权重，平均差小的学科以较小的权重。由于各种复杂因素的影响，同一科目的平均差在不同年度存在一定差异，为保持所测构念在不同年度上的稳定，在分数合成时，同一科目在不同年度应具有相同的权重，在计算各科权重时，应取不同年度的平均值。

具体做法是，先计算各年度每一科目的平均差，根据平均差计算各年度每一科目的权重，然后计算各年度每一科目权重的平均值，以此作为每一科目在不同年度分数合成时的权重。示例见表2。

表2  不同年度的科目权重与平均权重

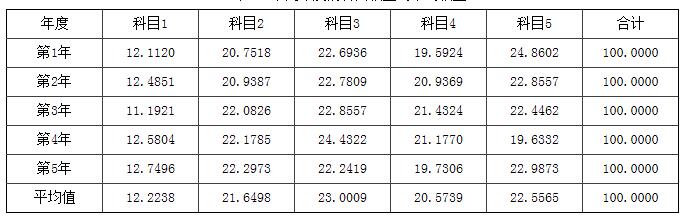
㈢分数合成过程分析

在分数合成中，要使分数合成过程能够实现所设计的构念，应注意以下几个方面。

在分数合成之前应进行分数转换，将原始分数转换成适合形式的导出分数，由于平均分和平均差会影响各科权重，各科导出分数应具有相同的平均分和平均差，这样各科在分数合成之前处在相同的起点上。

需要注意的是，要使导出分数具有相同的平均差，必须使用原始分数的平均差进行转换，即将各科原始分数除以各自的平均差，这样各科导出分数的平均差才相同。

导出分数究竟采用什么形式？需要考虑两个因素：一是分数的起点，通过平均分来确定，为了避免出现负数，应将平均分设定得大一些；二是分数单位，通过平均差来确定，既要对应试人员精确区分，又不出现小数，应将平均差设定得大一些，但又不能太大，否则计分就很复杂。

各科权重的选择要考虑到考试的目的和性质，尤其是对考试所测构念的理解和界定。不同目的和性质的考试对所测构念的理解和界定会有很大差别，应依据考试的实际情况，选择合理的确定权重的方法。一般来说，如果各个科目的满分不同，所测构念的重要性不同，须采用学科外部方法；如果学科外部方法不适用或无法使用，可以采用学科内部方法。

在分数转换与合成过程中，如果处理不当，会产生很多误差。一是在分数转换中，导出分数个数应大于或等于原始分数个数，例如，某一科目原始分数满分为100，没有小数，共有101个分数，在分数转换之后，导出分数个数应大于或等于101，这样原始分数才有可能一一对应到导出分数上，如果小于101，原始分数上必定有一些分数点在导出分数上找不到对应点，这些分数就会合并到一个点上，从而产生误差。二是在计算各科平均分、平均差、各科权重、导出分数的时候，要有足够的精度，比如取到小数点后八位，如果精度不够，也可能产生较大的误差。

四、结论

在分数转换中，由于考试分数对于应试人员的重要性，同时也由于原始分数难以服从正态分布，考试分数不适合进行正态转换，为了保持转换过程中的信息守恒，应采用线性转换的方法进行分数转换。

在分数合成中，由于各科平均差决定各科权重，应先通过分数转换将各科分数的平均差取齐，然后再选择学科外部或内部方法确定各科权重，在此基础上将各科分数合成为总分。

《中国考试》2005年第10期（上），第14-18页